Quantum annealing
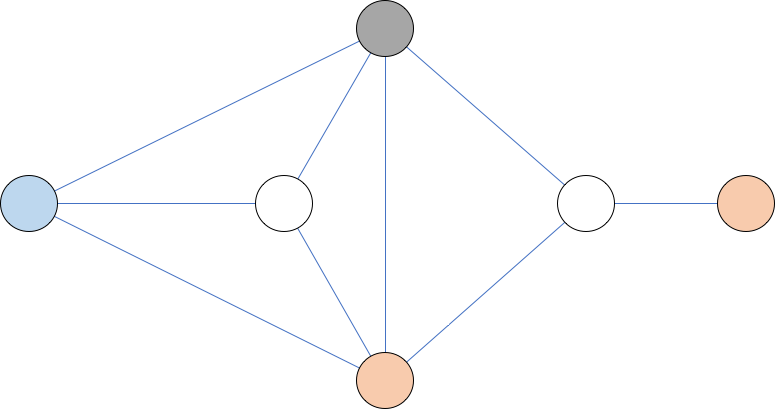
Quantum annealing is known as a quantum-mechanical approach for optimization problems. In quantum annealing approaches, the total Hamiltonian consists of driving and problem Hamiltonians. If we choose a driving Hamiltonian so that constraints are naturally satisfied without penalty terms, the dimension of the state space is considerably reduced. We call this method constrained quantum annealing. Especially, for graph coloring, whose ground state is degenerate, a quantum annealing approach based on real-time quantum dynamics has some advantages.
Localization sometimes occurs in a quantum annealing process. The model of constrained quantum annealing for graph coloring has an analogy with the Anderson model and provides a new viewpoint about localization in quantum annealing.
Reference
- Kazue Kudo, "Localization in the Constrained Quantum Annealing of Graph Coloring", J.Phys. Soc. Jpn. 89, 064001 (2020).
- Kazue Kudo, "Constrained quantum annealing of graph coloring", Phys. Rev. A 98, 022301 (2018).
[ Back to Top | Back to Home ]
Many-body localization
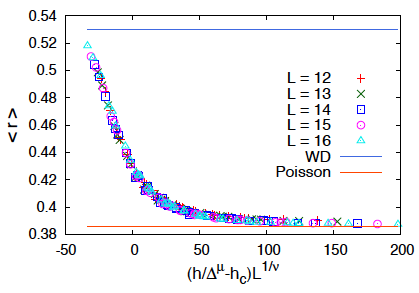
In many-body quantum systems with disorder, the dynamical transition from the thermal to many-body localization (MBL) phase occurs as disorder strength increases. On the other hand, dependence on interaction coupling is nontrivial. The MBL transition is characterized by the ratio of disorder strength to the power of interaction coupling with respect to an extra critical exponent.
Reference
- Kazue Kudo and Tetsuo Deguchi, "Finite-size scaling with respect to interaction and disorder strength at the many-body localization transition", Phys. Rev. B 97, 220201(R) (2018).
[ Back to Top | Back to Home ]
Quantum dynamics under periodic driving
We can observe a wide variety of quantum dynamics in one-dimensional quantum systems under periodic driving.
Cold atoms in an optical lattice in the presence of both static and oscillating linear fields, under some conditions, show large oscillations termed Super-Bloch Oscillations (SBOs). The tunneling amplitudes between adjacent lattices are renormalized, and the effective tunneling depends on the amplitude and frequency of the driving field. For full-understanding of features of SBOs, an important phase correction, which depends on the phase of the driving field as well as its frequency and amplitude, must be included.
Quantum transport in one-dimensional quantum systems that are described by, e.g., Heisenberg model and Hubbard model can be controlled by means of periodic driving. Some of the eigenstates of the undriven Hamiltonian are bound states, and others are unpaired states. The effective tunneling amplitudes (exchange interactions) are renormalized under an oscillating field, and the renormalized amplitudes are different between bound-pair and unpaired states. Thus, one can control the relative direction and speed of transport for bound-pair and unpaired states.
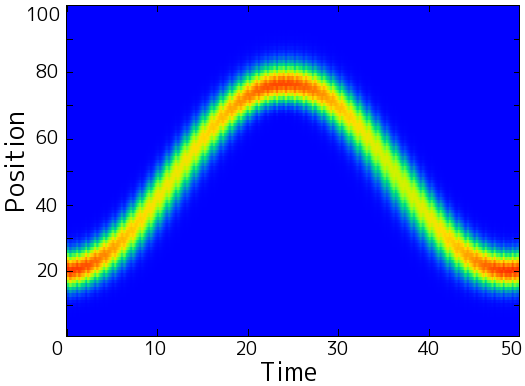
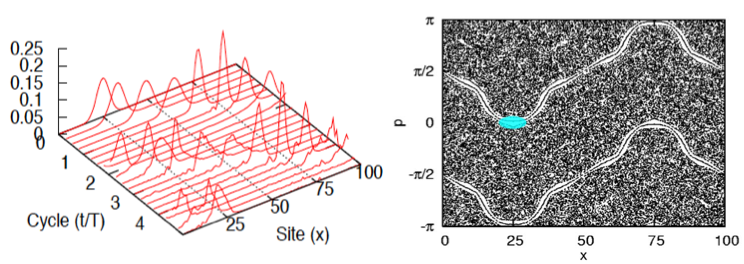
The one-magnon spin dynamics in a quantum spin system can give remarkable transfer of quantum information: a wavepacket travels for a quite long time without broadening under some conditions. The left figure below shows a one-magnon wavepacket dynamics in the quantum Heisenberg chain under an oscillating field. The non-diffusive transport is explained by the corresponding classical phase space. The quantum spin model is equivalent to the driven Harper model, which has the classical phase space, under a certain condition, shown in the right figure below. The colored region, which is on a shearless torus, corresponds to the initial position of the quantum wavepacket. The white channels in the chaotic sea include shearless tori, which are the key to make the quantum transport non-dispersive.
Frustrated quantum XXZ spin chains with next-nearest-neighbor couplings show Gaussian orthogonal ensemble (GOE) spectral statistics. The energy spectral flow for such a spin chain under an oscillating magnetic field has many avoided crossings which lead to energy diffusion. Energy diffusion for the system depends on both the field strength and driving frequency. The diffusion coefficients obey the power law, whose power varies depending on the linear response and nonperturbative regimes, with respect to the strength and frequency of the field. The widths of the linear response and the nonperturbative regimes depend on the strength of frustrations.
References
- K. Kudo and T.S. Monteiro, "Theory of super-Bloch oscillations", Phys. Rev. A 83, 053627 (2011).
- K. Kudo, T. Boness, and T.S. Monteiro, "Control of bound-pair transport by periodic driving", Phys. Rev. A 80, 063409 (2009).
- T. Boness, K. Kudo, and T.S. Monteiro, "Doubly excited ferromagnetic spin chain as a pair of coupled kicked rotors", Phys. Rev. E 81, 046201 (2010).
- K. Kudo and T.S. Monteiro, "Quantum transport and spin dynamics on shearless tori", Phys. Rev. E 77, 055203(R) (2008).
- Kazue Kudo and Katsuhiro Nakamura, "Energy diffusion in frustrated quantum spin chains exhibiting Gaussian orthogonal ensemble level statistics", Phys. Rev. B 71, 144427 (2005).
[ Back to Top | Back to Home ]
Level statistics
Level statistics of quantum systems generally show the Poisson distribution in a level-spacing distribution when the corresponding classical system is integrable. By contrast, the typical level-spacing distribution for a non-integrable system is the Wigner distribution. A quantum XXZ spin chain (anisotropic Heisenberg model) is integrable by the Bethe ansatz, although it does not have a corresponding classical system. Its level-spacing distribution is the Poisson distribution, and that of the XXZ spin chain with next-nearest-neighbor couplings, which is not solvable by the Bethe ansatz, is the Wigner distribution. This implies that the level statistics can be used to check the Bethe ansatz solvability. However, non-integrable quantum systems show non-Wigner distributions in some cases due to imperfect desymmetrization or finite size effects.
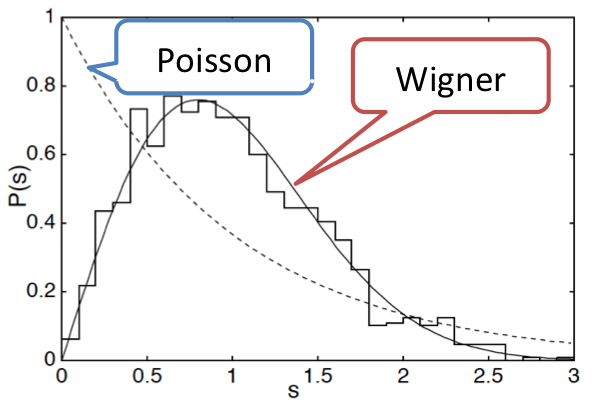
It was known that the level statistics of a standard Dicke model changes under quantum phase transition (QPT). We have investigated the level statistics of a pseudo-Hermitian Dicke Hamiltonian, which has real-number eigenvalues though it is not Hermitian. Its level-spacing distribution near the integrable limit is close to Poisson distribution, while it is Wigner distribution for the ranges of the parameters for which the Hamiltonian is non-integrable. The assertion that QPT is a precursor to a change in the level statistics, which is true in the standard Dicke model, is valid for the pseudo-Hermitian Dicke model only for a limited range of the parameter space because of its larger parameter space.
References
- Kazue Kudo and Tetsuo Deguchi, "Unexpected non-Wigner behavior in level spacing distributions of next-nearest-neighbor coupled XXZ spin chains", Phys. Rev. B 68, 052510 (2003).
- Kazue Kudo and Tetsuo Deguchi, "Level statistics of XXZ spin chains with a random magnetic field", Phys. Rev. B 69, 132404 (2004).
- Kazue Kudo and Tetsuo Deguchi, "Level Statistics of XXZ Spin Chains with Discrete Symmetries: Analysis through Finite-size Effects", J. Phys. Soc. Jpn. 74, 1992-2000 (2005).
- Tetsuo Deguchi, Pijush K. Ghosh, and Kazue Kudo, "Level statistics of a pseudo-Hermitian Dicke model", Phys. Rev. E 80, 026213 (2009).
[ Back to Top | Back to Home ]
Wrinkle formation on coatings
Wrinkles often emerge when double coating is applied. Considering wrinkle formation as buckling of an elastic thin film, we proposed a simple mathematical model. The mathematical model explains phenomena at early stage of wrinkle formation. Numerical simulations demonstrate reproduction of wrinkle formation.
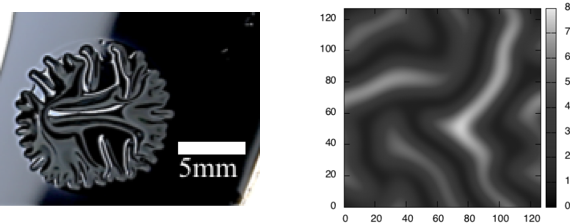
Reference
- Michiko Shimokawa, Hikaru Yoshida, Takumi Komatsu, Rena Omachi and Kazue Kudo, "Emergence of Wrinkles during the Curing of Coatings", Gels 4, 41 (2018).
[ Back to Top | Back to Home ]
Magnetic domain pattern on a Co/Ni multilayer
The experiment by means of spin-polarized low energy electron microscopy (SPLEEM) has shown that the magnetic anisotropy, and hence magnetic domain patterns, in a Co/Ni multilayer changes depending on the number of layers. In the experiment, pairs of 2-ML-thick Ni and 1-ML-thick Co layers were deposited on W(110). Perpendicular magnetization appears after the deposition of Ni layers. In contrast, in-plane magnetization appears after Co deposition for the first and second pairs. However, after the deposition of the third Co/Ni pair, magnetization remains perpendicular to the surface even after Co deposition. When domain patterns appear in the perpendicular magnetization images, the in-plane magnetization images show clear domain-wall structures. The numerical simulation, which is based on the Landau-Lifshitz-Gilbert (LLG) equation, well reproduce magnetic domain patterns with clear domain walls and the change in magnetic anisotropy.

References
- Masahiko Suzuki, Kazue Kudo, Kazuki Kojima, Tsuneo Yasue, Noriko Akutsu, Wilson Agerico Diño, Hideaki Kasai, Ernst Bauer and Takanori Koshikawa, "Magnetic domain patterns on strong perpendicular magnetization of Co/Ni multilayers as spintronics materials: I. Dynamic observations", J. Phys.: Condens. Matter 25, 406001 (2013).
- Kazue Kudo, Masahiko Suzuki, Kazuki Kojima, Tsuneo Yasue, Noriko Akutsu, Wilson Agerico Diño, Hideaki Kasai, Ernst Bauer and Takanori Koshikawa, "Magnetic domain patterns on strong perpendicular magnetization of Co/Ni multilayers as spintronics materials: II. Numerical simulations", J. Phys.: Condens. Matter 25, 395005 (2013).
[ Back to Top | Back to Home ]
Magnetic domain pattern in a spinor BEC
When a Bose-Einstein condensation (BEC) has spin degrees of freedom, it is called a spinor BEC. In spinor BECs, spin and gauge degrees of freedom couple in various manners, leading to nontrivial properties of spin waves and topological excitations such as spin textures and vortices. The figures show examples of magnetic domain patterns (left: transverse magnetization, right: longitudinal magnetization) that are simulated by means of the Gross-Pitaevskii (GP) equation.
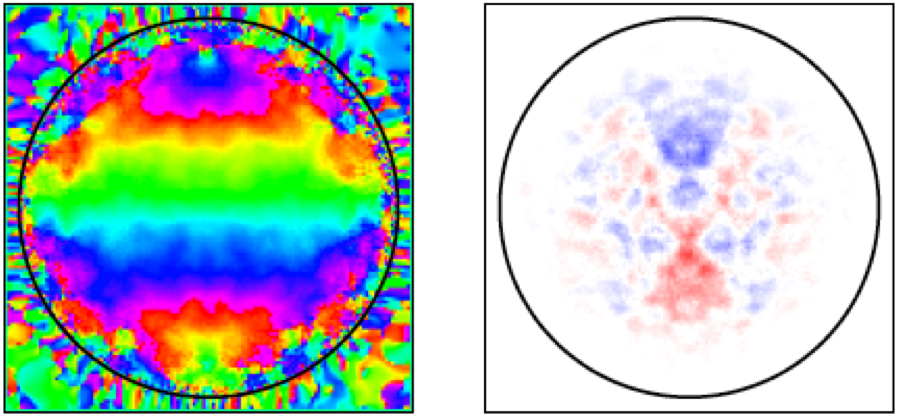
If we focus on spin degrees of freedom, we can derive a hydrodynamic equation from the GP equation under some assumptions. The hydrodynamic description extracts the dynamics of spin wave and affords a straightforward approach by which to investigate the spin dynamics of the condensate.
The hydrodynamic equation with dissipation has the same form as the equation of the spin dynamics in a conducting ferromagnet. Thus, the domain pattern which is similar to that of a ferromagnetic thin film can be reproduced by the hydrodynamic equation simulation.
References
- Yuki Kawaguchi, Hiroki Saito, Kazue Kudo, and Masahito Ueda, "Spontaneous magnetic ordering in a ferromagnetic spinor dipolar Bose-Einstein condensate", Phys. Rev. A 82, 043627 (2010).
- Kazue Kudo and Yuki Kawaguchi, "Hydrodynamic equation of a spinor dipolar Bose-Einstein condensate", Phys. Rev. A 82, 053614 (2010).
- Kazue Kudo and Yuki Kawaguchi, "Dissipative hydrodynamic equation of a ferromagnetic Bose-Einstein condensate: Analogy to magnetization dynamics in conducting ferromagnets", Phys. Rev. A 84, 043607 (2011).
- Kazue Kudo and Yuki Kawaguchi, "Magnetic domain growth in a ferromagnetic Bose-Einstein condensate: Effects of current", Phys. Rev. A 88, 013630 (2013).
- Kazue Kudo and Yuki Kawaguchi, "Coarsening dynamics driven by vortex-antivortex annihilation in ferromagnetic Bose-Einstein condensates", Phys. Rev. A 91, 053609 (2015).
[ Back to Top | Back to Home ]
Domain pattern in a ferromagnetic thin film
Ferromagnetic garnet thin films show domain patterns, which consist of up-spin and down-spin domains. In order to observe the magnetic domain patterns under a zero field in experiments, usually an external magnetic field is applied once up to the saturation field, and then it is removed. The characteristics of domain patterns depend on the decreasing rate of the external field. When the field decreases rapidly, a sea-island structure (right figure) appears, while a labyrinth structure (left figure) is observed for a slowly decreasing field.

Under an oscillating field, we can see some interesting patterns such as lattice patterns, concentric-ring patterns and traveling patterns moving very slowly compared with the frequency of the field. The key idea to analyze the effect of the oscillating field on these patterns is to separate the dynamics into a rapidly oscillating part and a slowly varying part.
The Landau-Lifshitz-Gilbert (LLG) equation is often used for simulation of magnetic domain patterns. If the Gilbert damping is removed from the LLG equation, it merely describes the precession of magnetization with a ferromagnetic interaction. However, even without the damping, domains that look similar to those of scalar fields are formed.
References
- Kazue Kudo, Michinobu Mino and Katsuhiro Nakamura, "Magnetic Domain Patterns Depending on the Sweeping Rate of Magnetic Fields", J. Phys. Soc. Jpn 76, 013002 (2007).
- Kazue Kudo and Katsuhiro Nakamura, "Field sweep-rate dependence of magnetic domain patterns: Numerical simulations for a simple Ising-like model", Phys. Rev. B 76, 054111 (2007).
- Kazue Kudo and Katsuhiro Nakamura, "Effects of an oscillating field on the pattern formation in a ferromagnetic thin film: Analysis of patterns traveling at a low velocity", Phys. Rev. E 76, 036201 (2007).
- Kazue Kudo, "Effects of an oscillating field on magnetic domain patterns: Emergence of concentric-ring patterns surrounding a strong defect", Phys. Rev. E 80, 016209 (2009).
- Kazue Kudo, "Effects of Landau-Lifshitz-Gilbert damping on domain growth", Phys. Rev. E 94, 062215 (2016).
[ Back to Top | Back to Home ]
Semi-automatic timetabling
Scheduling parallel sessions of an academic meeting is a complicated task. Organizers have to consider a lot of constraints. For example, sessions with the same topic and those with largely overlapped audiences should not be in the same timeslot; some sessions often need to avoid particular timeslots; and the number of meeting rooms is often limited. If each presentation is assigned to an appropriate session, an antiferromagnetic Potts model can be used for semi-automatic timetabling.

Reference
- Kazue Kudo, "Academic Meeting Scheduling Using an Antiferromagnetic Potts Model", J. Phys. Soc. Jpn. 86, 075002 (2017).
[ Back to Top | Back to Home ]