量子アニーリング
量子アニーリングは,組み合わせ最適化問題を解くための量子力学的手法として使われています. 系の対称性を利用して制約条件が自然に満たされるように,量子ゆらぎの項を工夫して設定すると,計算に必要が空間の次元を大幅に削減することができます. この方法を制約量子アニーリングと呼びます. 特に,解が多数あるグラフ彩色問題を解く場合には,実時間発展による制約量子アニーリングの手法が有利になる場合があります.
量子アニーリングの過程では,局在現象が起こりうることが知られています. 制約量子アニーリングをグラフ彩色問題に適用したモデルは, アンダーソン模型とのアナロジーの観点から局在現象を見ることもできます.
参考文献
- Kazue Kudo, "Localization in the Constrained Quantum Annealing of Graph Coloring", J.Phys. Soc. Jpn. 89, 064001 (2020).
- Kazue Kudo, "Constrained quantum annealing of graph coloring", Phys. Rev. A 98, 022301 (2018).
[ このページのトップへ | ホームへ戻る ]
多体局在転移
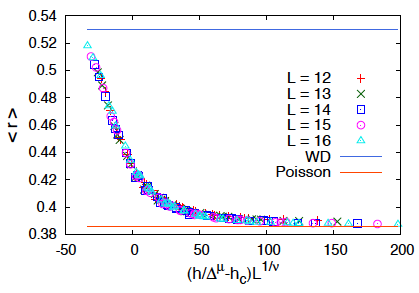
相互作用のある量子多体系に乱れ(disorder)があるとき, 一定の相互作用の下で乱れを大きくしていくと, 熱平衡相から多体局在相への転移が起こります. その一方で,この転移の相互作用への依存性は,単純ではありません. 乱れの強さと相互作用パラメタの冪乗との比を用いて有限サイズスケーリングを行うと, 準位統計の指標が一本の曲線に重なる領域が現れます.
参考文献
- Kazue Kudo and Tetsuo Deguchi, "Finite-size scaling with respect to interaction and disorder strength at the many-body localization transition", Phys. Rev. B 97, 220201(R) (2018).
[ このページのトップへ | ホームへ戻る ]
振動外場下の量子ダイナミクス
量子1次元系に振動外場を加えると,元の系の性質が変化し, 多種多様なダイナミクスを観察することができます.
光格子中の冷却原子に,定常外場と振動外場をある条件を満たすように加えると,スーパーブロッホ振動と呼ばれる大振幅のゆっくりした振動が観察されます. その振幅は,振動磁場の振幅と振動数の比に依存します. また,スーパーブロッホ振動の振動数や位相は,定常外場および振動外場の振動数と位相に依存します.
量子1次元ハイゼンベルク模型やハバード模型の固有状態は,相互作用の強い(z方向の異方性が強い)ときには,固有状態が束縛状態と散乱状態とに分かれる場合があります. この系に振動磁場を加えると,実効的な交換相互作用が変化しますが,束縛状態と散乱状態では,それぞれ変化の仕方が異なります. 初期に両方の成分を含んだ量子波束を用意して振動磁場を加えると,それぞれの進む方向やスピードを制御できるため,もとの波束を2つの成分の波束に振り分けることができます.
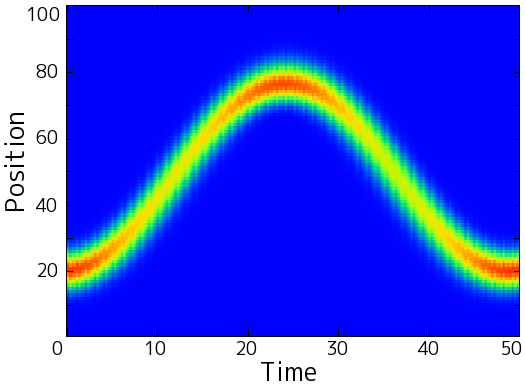
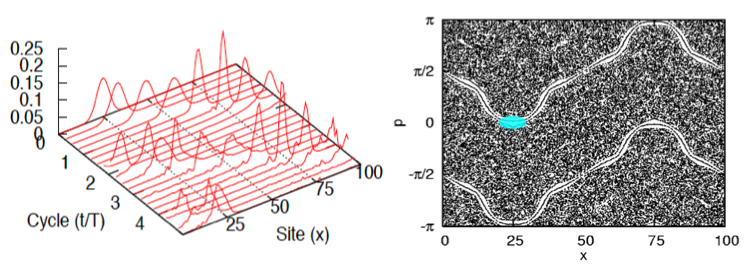
量子1次元ハイゼンベルク模型(スピン1/2)の単励起の場合は,1粒子系と見なせます. この系に,定在波型の振動磁場を加えたときの量子波束のダイナミクスは,対応する古典系の位相空間断面の性質から予測することができます. 例えば,波束があまり広がらずに伝送するように振幅,振動数を設定すると,下図の左のような量子スピン波束のダイナミクスが見られます. これに対応する古典模型を用いて,振動磁場の1周期ごとに位置xと運動量pをプロットしたポアンカレ断面が,下図の右です. 右図の楕円部分[(x,p) = (25,0) 付近]が,量子波束の初期位置に対応します. この初期波束は白く見えるトーラス部分に位置していて,それが波束の崩れにくさと関係しています.
次近接相互作用まで含む量子1次元XXZスピン模型に,進行波形の振動磁場を加えると,エネルギー・スペクトルの準位間隔の狭いところで遷移が次々と起こり,基底状態にあった初期状態が,エネルギー空間を広がっていきます(エネルギー拡散). エネルギー拡散は,磁場の強さや振動数,そして次近接相互作用の大きさ(フラストレーションの強さ)に依存します. 磁場の強さと振動数の積に対して拡散定数をプロットすると,通常拡散が起こる線形応答領域と,異常拡散の起こる非摂動領域があることが分かります. それらの領域の幅はフラストレーションの強さに依存します.
参考文献
- K. Kudo and T.S. Monteiro, "Theory of super-Bloch oscillations", Phys. Rev. A 83, 053627 (2011).
- K. Kudo, T. Boness, and T.S. Monteiro, "Control of bound-pair transport by periodic driving", Phys. Rev. A 80, 063409 (2009).
- T. Boness, K. Kudo, and T.S. Monteiro, "Doubly excited ferromagnetic spin chain as a pair of coupled kicked rotors", Phys. Rev. E 81, 046201 (2010).
- K. Kudo and T.S. Monteiro, "Quantum transport and spin dynamics on shearless tori", Phys. Rev. E 77, 055203(R) (2008).
- Kazue Kudo and Katsuhiro Nakamura, "Energy diffusion in frustrated quantum spin chains exhibiting Gaussian orthogonal ensemble level statistics", Phys. Rev. B 71, 144427 (2005).
[ このページのトップへ | ホームへ戻る ]
準位統計
一般に量子系の準位間隔分布(準位統計)は,対応する古典系が可積分ならばポアソン分布を,非可積分ならウィグナー分布を示すとされています. 量子XXZスピン鎖(異方的ハイゼンベルク模型)は,対応する古典系はありませんが,ベーテ仮説で厳密に解ける可積分の模型です. これに次近接相互作用やランダム磁場を加えると,非可積分になります. これらの模型で準位統計を調べた結果,可積分ではポアソン分布,非可積分ではウィグナー分布を示すことが分かりました. つまり準位統計は,ベーテ仮説の意味での可積分性を判断する基準にもなります. ただし,その関係が見かけ上くずれる場合もあります. その理由としては,不完全な非対称化,あるいは有限サイズ効果が挙げられます.
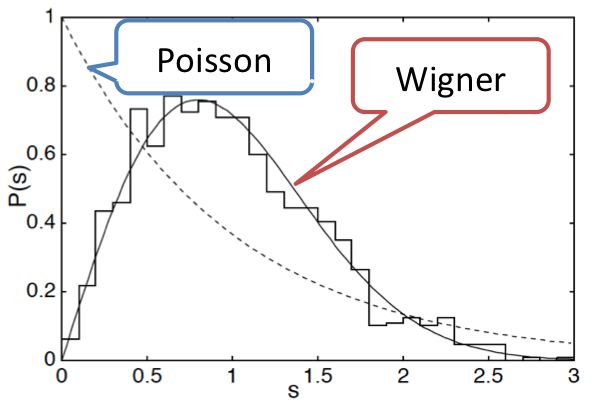
Dicke模型では, 量子相転移が準位統計の変化と深く関連していることが確認されています. この模型を拡張した擬エルミート(pseudo-Hermitian)Dicke模型は,非エルミートながら全ての固有値が実数です. 擬エルミートDicke模型では,量子相転移と準位統計の変化との対応関係が,ある限られたパラメタ領域でのみ成り立ちます. それは,擬エルミート模型が,通常のエルミート模型よりも大きなパラメタ空間を持つことに起因します.
参考文献
- Kazue Kudo and Tetsuo Deguchi, "Unexpected non-Wigner behavior in level spacing distributions of next-nearest-neighbor coupled XXZ spin chains", Phys. Rev. B 68, 052510 (2003).
- Kazue Kudo and Tetsuo Deguchi, "Level statistics of XXZ spin chains with a random magnetic field", Phys. Rev. B 69, 132404 (2004).
- Kazue Kudo and Tetsuo Deguchi, "Level Statistics of XXZ Spin Chains with Discrete Symmetries: Analysis through Finite-size Effects", J. Phys. Soc. Jpn. 74, 1992-2000 (2005).
- Tetsuo Deguchi, Pijush K. Ghosh, and Kazue Kudo, "Level statistics of a pseudo-Hermitian Dicke model", Phys. Rev. E 80, 026213 (2009).
[ このページのトップへ | ホームへ戻る ]
塗膜のシワ形成
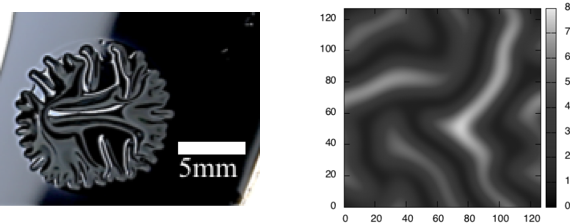
塗料が十分乾いてない状態で重ね塗りすると,シワができてしまう場合があります. 上塗りの塗料から染み出した溶剤が下塗りの塗膜を膨潤させた結果,塗膜に応力がかかるためです. このシワ形成を弾性薄膜の座屈現象とみなして数理モデルで表現し,それを用いて数理解析を行うと,シワ形成の初期段階の現象をよく説明できます. また,数値シミュレーションによって,シワの形成される様子を再現することもできます.
参考文献
- Michiko Shimokawa, Hikaru Yoshida, Takumi Komatsu, Rena Omachi and Kazue Kudo, "Emergence of Wrinkles during the Curing of Coatings", Gels 4, 41 (2018).
[ このページのトップへ | ホームへ戻る ]
Co/Ni多層膜における積層過程の磁区パターン
Co/Ni多層膜では,表面に垂直方向の磁化が現れ磁区パターンが観察できます. スピン偏極低エネルギー電子顕微鏡(spin polarized low energy electron microscopy, SPLEEM)による実験では,Coを1原子層とNiを2原子層のペアをW(110)基板上に積層していくと,初めのうちは積層するごとに磁気異方性が面内→面直→面内と変化し,積層ペアが増えると面直方向の磁化が安定になる様子が観察されました. この磁区パターンの変化をLandau-Lifshitz-Gilbert(LLG)方程式を用いて数値シミュレーションすると,くっきりとした磁壁など実験で観察された磁区パターンの特徴が再現できます.

参考文献
- Masahiko Suzuki, Kazue Kudo, Kazuki Kojima, Tsuneo Yasue, Noriko Akutsu, Wilson Agerico Diño, Hideaki Kasai, Ernst Bauer and Takanori Koshikawa, "Magnetic domain patterns on strong perpendicular magnetization of Co/Ni multilayers as spintronics materials: I. Dynamic observations", J. Phys.: Condens. Matter 25, 406001 (2013).
- Kazue Kudo, Masahiko Suzuki, Kazuki Kojima, Tsuneo Yasue, Noriko Akutsu, Wilson Agerico Diño, Hideaki Kasai, Ernst Bauer and Takanori Koshikawa, "Magnetic domain patterns on strong perpendicular magnetization of Co/Ni multilayers as spintronics materials: II. Numerical simulations", J. Phys.: Condens. Matter 25, 395005 (2013).
[ このページのトップへ | ホームへ戻る ]
スピノルBECの磁区パターン
スピン自由度を持つボース-アインシュタイン凝縮(BEC)では,強磁性相互作用などの効果により,磁区パターンが現れることがあります. たとえば,多成分のGross-Pitaevskii方程式を用いた数値シミュレーションで,図のような磁区パターンを生成することができます (左図: 横磁化, 右図: 縦磁化).
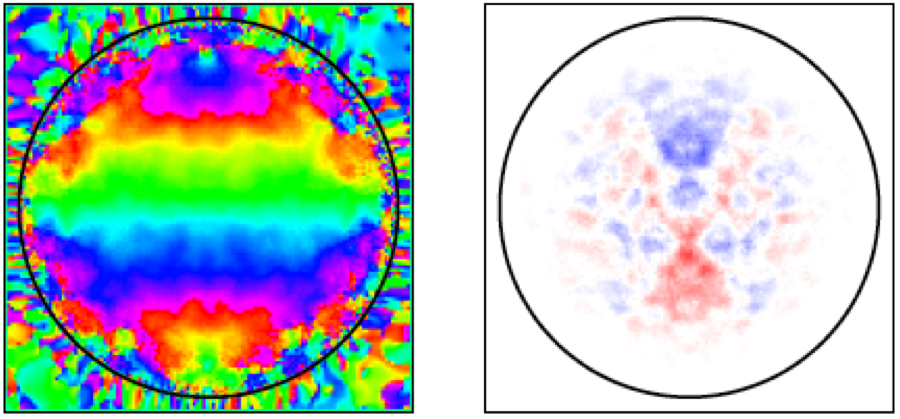
また,ある仮定のもとでは,スピンの自由度だけに着目することで,流体方程式という簡潔な形の方程式に書き換えることができます. 流体方程式を用いると,スピンのダイナミクスに関して,より直観的でストレートな理論解析が可能になります.
また,散逸のある場合の流体方程式は,金属磁性体のスピンダイナミクスを記述する方程式と同じ形をしています. このため,強磁性薄膜で見られたのと同様な磁区パターンを再現することもできます.
参考文献
- Yuki Kawaguchi, Hiroki Saito, Kazue Kudo, and Masahito Ueda, "Spontaneous magnetic ordering in a ferromagnetic spinor dipolar Bose-Einstein condensate", Phys. Rev. A 82, 043627 (2010).
- Kazue Kudo and Yuki Kawaguchi, "Hydrodynamic equation of a spinor dipolar Bose-Einstein condensate", Phys. Rev. A 82, 053614 (2010).
- Kazue Kudo and Yuki Kawaguchi, "Dissipative hydrodynamic equation of a ferromagnetic Bose-Einstein condensate: Analogy to magnetization dynamics in conducting ferromagnets", Phys. Rev. A 84, 043607 (2011).
- Kazue Kudo and Yuki Kawaguchi, "Magnetic domain growth in a ferromagnetic Bose-Einstein condensate: Effects of current", Phys. Rev. A 88, 013630 (2013).
- Kazue Kudo and Yuki Kawaguchi, "Coarsening dynamics driven by vortex-antivortex annihilation in ferromagnetic Bose-Einstein condensates", Phys. Rev. A 91, 053609 (2015).
[ このページのトップへ | ホームへ戻る ]
強磁性薄膜の磁区パターン形成
強い一軸異方性を持つ強磁性薄膜では,上向きと下向きのスピンによる磁区パターンを観察することができます. いったん飽和磁場以上の磁場を印加した後で,ゼロ磁場まで磁場を掃引すると,図のような特徴的な長さを持った磁区パターンが現れる場合があります. このとき,掃引速度が速いと左図のような海島構造が,遅いと右図のような迷路構造が観察されます. 簡単な理論模型を用いたシミュレーションでも,同様のパターンが再現できます. [→ もっと詳しく]

振動磁場中では,格子状や同心円上のパターン, 振動の速さに比べて非常にゆっくりと並進する磁区パターンなど, さらに興味深いパターンが見られます. 振動外場がパターン形成に及ぼす影響を理論的に議論するには, 扱う変数を,速く振動する部分と遅く変化する部分に分けて考え, 振動磁場の影響を遅い変数の方程式に取り込んで解析する方法があります.
Landau-Lifshitz-Gilbert (LLG)方程式を用いても,同様の磁区パターンが再現できます. LLG方程式にはGilbert減衰と呼ばれる項があります. この減衰項がなければ単なる歳差運動の方程式になるのですが, 不思議なことに,減衰項の有無にかかわらず磁区パターンが形成されます.
参考文献
- Kazue Kudo, Michinobu Mino and Katsuhiro Nakamura, "Magnetic Domain Patterns Depending on the Sweeping Rate of Magnetic Fields", J. Phys. Soc. Jpn 76, 013002 (2007).
- Kazue Kudo and Katsuhiro Nakamura, "Field sweep-rate dependence of magnetic domain patterns: Numerical simulations for a simple Ising-like model", Phys. Rev. B 76, 054111 (2007).
- Kazue Kudo and Katsuhiro Nakamura, "Effects of an oscillating field on the pattern formation in a ferromagnetic thin film: Analysis of patterns traveling at a low velocity", Phys. Rev. E 76, 036201 (2007).
- Kazue Kudo, "Effects of an oscillating field on magnetic domain patterns: Emergence of concentric-ring patterns surrounding a strong defect", Phys. Rev. E 80, 016209 (2009).
- Kazue Kudo, "Effects of Landau-Lifshitz-Gilbert damping on domain growth", Phys. Rev. E 94, 062215 (2016).
[ このページのトップへ | ホームへ戻る ]
学会のプログラム編成の半自動化
複数の会場で講演が同時進行する学会や研究会のプログラム編成は,複雑で大変な作業です. 同じ時間に重ねてはいけないセッションの組み合わせや,特定の時間枠を避けるなどの制約を考慮して編成しなければなりません. 各講演が適切なセッションに割り振られていれば,それぞれのセッションに時間枠を割り当てる作業は,反強磁性ポッツ模型を利用して半自動化することができます. [→ もっと詳しく]

参考文献
- Kazue Kudo, "Academic Meeting Scheduling Using an Antiferromagnetic Potts Model", J. Phys. Soc. Jpn. 86, 075002 (2017).
[ このページのトップへ | ホームへ戻る ]